机器视觉：Asymmetry Problem in Computer Vision

自然法则无时不刻不给予着人类以对称性的恩惠，从一片树叶到人类自身，其形态都是对称的。对称性的特性，大大减轻了人类的记忆和认知负担。然而，弱相互作用中互为镜像的物质的运动不对称却暗藏着自然法则对非对称性的偏爱。

在计算机视觉中，对称性是一个很好的先验，如果某一个特定的物体具备对称性的话，通过引入对称性可以提升系统的精度。常见的对称性包括：

物体本身具备对称性，且这种对称性不容易受大视角变化的影响。主要应用场景为在训练诸如检测模型的时候，可以将这一信息加入到训练样本的扩增上；
相似性度量具备对称性。这种对称性常体现在设计的相似性度量准则上，A与B计算出的相似性和B与A得到的相似性是一样。

我们的大脑深受对称性法则的影响，所以对于第一种情况，我们可以非常直观的将这一法则应用到我们的视觉模型训练中，但是对于第二种情况，特别是当相似性度量由非对称性在对称性上转化而来的时候，我们的第一意识却频频出错。计算机视觉中非对称现象和非对称相似性度量如此干扰我们的第一意识，以至于小白菜对这个问题曾做出过若干的思考，下面是小白菜结合自己的一些思考和经验做的总结和整理。

局部特征匹配中的非对称问题

在用局部特征进行匹配的时候，比如SIFT，用A图匹配B图和用B图匹配A图，得到的匹配结果是不一样的，如下图所示：

在这匹配的过程中，所有的度量方式比如最近邻、次近邻、几何校验等都是具备对称性的，所以很容易给我们造成一种错觉就是他们的匹配结果应该是一样的。这里面造成匹配结果不对称的根本因素在于A图和B图它们的局部特征数目是不相等的，比如A有500个局部特征，B有800个局部特征，用500个局部特征去匹配800局部个特征和用800个局部特征去匹配500个局部特征，势必造成匹配的结果不一样。一个鲁棒的匹配算法，应该在用A匹配B和用B匹配A时都能获得比较好的匹配结果，以避免单一结果匹配较好的情形，像下面的匹配算法就不是一种好的匹配算法：

在设计匹配算法的时候，我们应避免我们的算法出现单一匹配好的情形，以提高匹配的鲁棒性。如需获取上图匹配结果，可以访问covdet获取。

Logo识别中的非对称问题

Logo的识别问题，可以分为两类:

基于检测的方式
基于检索的方式

基于检测方式的缺点在于新的Logo样式来临时，会面临训练样本如何获取以及人工标注的问题，虽然可以自动通过往图片上贴Logo的方式来构造训练样本，但这种方式容易造成过拟合；基于检索的方式的优点在于，它不会面临训练样本获取和标注的问题，能够以较快的速度响应新Logo检测的请求，但是基于Logo检索的方式，面临一个很大的问题就是尺寸不对称性。

这种尺寸不对称性体现在：对于待检测的图片，Logo所占的区域是很小的，通常区域面积占总体面积比的5%都不到，这样就导致提取的Logo区域的特征（比如局部特征）被非Logo区域的特征给“淹没”掉，如下图所示：

上图这个图选取得不是很合适，因为背景比较干净，Logo区域的特征还是其了比较大的作用。对于一般的情况，由于Logo区域的特征被非Logo区域的特征给淹没掉，从而使得在Logo库里检索的时候，在top@K（K取得比较小）里面比较难以检索到相关的Logo，而且即便是做重排，也比较难以将最相关的Logo排到最前面。

针对这种由于尺寸不对称性造成的有用特征（信号）被无用信号淹没的问题，很难在不对检索精度造成较大影响的前提下找到比较有效的解决办法。如果要剔除无用信号造成的干扰，一种比较好的方法是先进行粗略的检测，这一步不要求检测的准确率很高，只要保证召回率很高即可，然后可以根据定位到的框提取特征，再进行检索以及校验。这种方式由于剔除了非相关区域特征的干扰，所以准确率和召回率通常能够得到较好的保证，唯一不足的是，引入了检测，而检测势必要求对数据进行标注（半自动）。不过总体来说，这仍然是一种非常不错的方法。

PQ中的非对称距离

在此前的文章图像检索：再叙ANN Search中，小白菜曾对PQ做过比较详细的介绍，这里对PQ中非对称距离的计算做一详述。

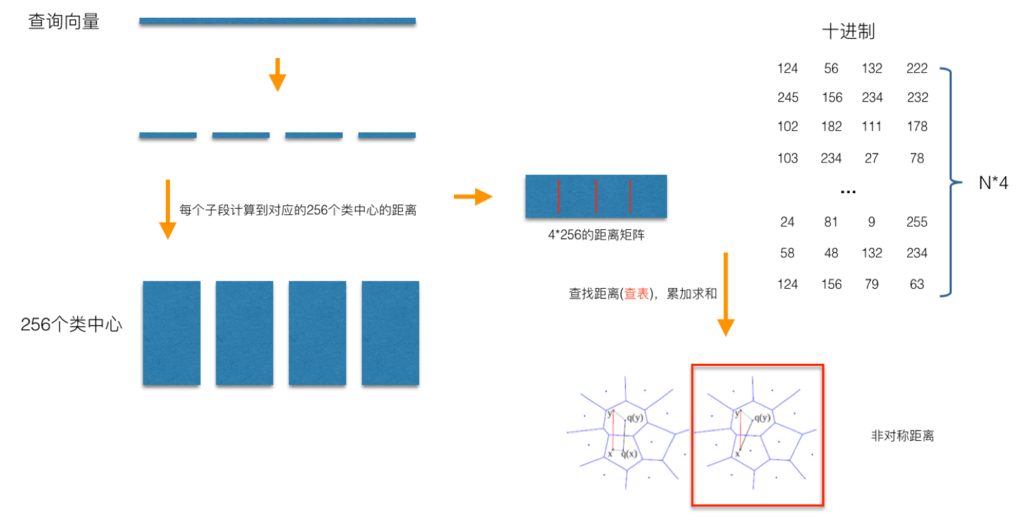
如上图所示，非对称距离计算方式（红框标示）在计算查询向量$x$到库中某一样本$y$之间的距离时，并不需要对查询向量$x$自身进行量化，而是直接计算查询向量$x$到量化了的$y$之间的距离，这种距离计算方式可以确保非距离计算方式以更大的概率保证计算的距离更接近于真实的距离（与对称距离计算方式相比较），而且这种方式比对称距离计算方式在实施的过程中，来得更直接，因为我们不需要对查询向量进行量化，而是直接计算到对应子段之间的距离，然后采用查表的方式获取到查询向量到库中所有样本的距离。这种通过查表的方式，是PQ能够加速距离计算的核心。

非对称性的应用，在这里展示了它有利的一面，通过将非对称性延展到相似性度量上，可以进一步缩小量化造成的损失。既然谈到了PQ的思想，我们还可以对PQ的改进做一下的延拓。

Polysemous Codes

PQ的改进版本很多，比如OPQ, Jegou等人又在PQ的基础上对PQ计算距离的过程中做了进一步加速，提出了Polysemous Codes（中译为“一词多义编码”，为何叫Polysemous Codes，容小白菜慢慢道来)。

前面已经提到，即便是采用查表的方式，仍然还是要查表挨个对库中的每个样本计算到查询向量之间的距离，这种距离能不能转换成汉明距离的计算？正如上图所示的，对于每个向量，我们可以知道它对应的量化索引编码，如果这个量化索引编码本身就是一种汉明编码，那么我们就可以直接用通过计算汉明距离来得到粗排序的结果，然后再对topK的结果计算ADC距离，Polysemous Codes的动机正是如此，实际上Polysemous Codes不仅充当了量化索引编码，还充当了一个快速过滤的作用。

应该说，对于所有的相似性度量距离，汉明距离计算从效率上来讲，是最快的。在faiss的项目wiki的re-filtering PQ codes with polysemous codes有结论：

It is about 6x faster to compare codes with Hamming distances than to use a product quantizer.

也就是计算一次PQ的距离，跟计算一次汉明距离计算相比，会慢6倍左右，说明如果能把PQ编码赋予汉明编码的意义的话，距离的计算会提升6倍，这个提升还是非常巨大的。Polysemous Codes的实现已在Faiss中Polysemous Codes Implementation。下图解释一下“Polysemous Codes”的“Polysemous”，即一词多义：

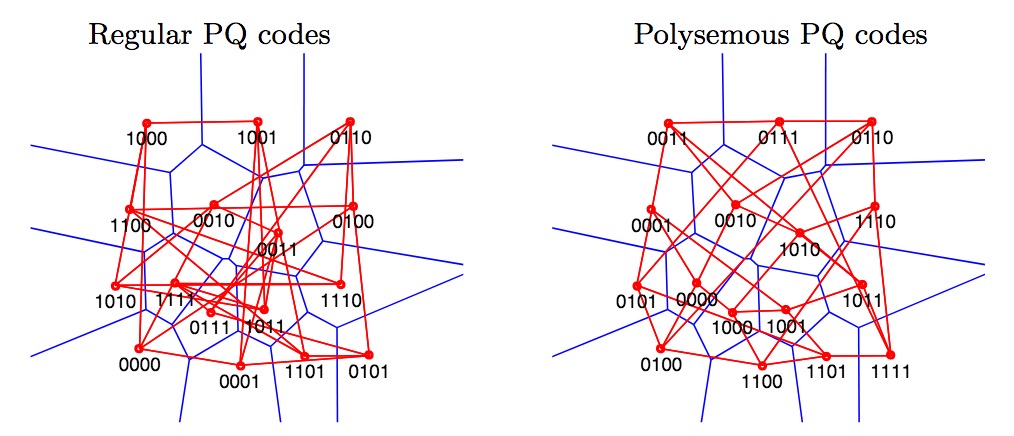
Polysemous codes are compact representations of vectors that can be comparedeither with product quantization (222M distance evaluations per second per core for 8-byte codes) or as binary codes (1.19G distances per second). To obtain this property, we optimize the assignment of quantization indexes to bits such that closest centroidshave a small Hamming distance. 【摘自Polysemous Codes】

在标准的PQ编码中，编码仅指代对应的量化索引编码，即由哪个类中心来近似该子段向量，比如上面的左图，4位的二进制编码仅表示类中心编码（编号），除此之外，无任何其他的意义；而在Polysemous Codes中，如右图所示，它不仅能表示类中心的编码（编号），而且它还是一种汉明编码，从这里可以看到，该编码包含了两种特性，我们既可以计算PQ距离，又可以计算汉明距离，因而该编码被称为“Polysemous Codes”是非常妥帖的。由于计算汉明距离更高效，而Polysemous Codes又是一种汉明码，我们可以先用汉明距离进行粗排序，在采用PQ距离进行重排。

Polysemous Codes所拥有的这两种特性，不能不感叹它是极其优雅美丽的。

累计最小（最大）距离非对称问题

在度量两个集合的相似性的时候，累计最小（最大）距离是一个比较好用的相似性度量距离。假设两个集合分别为$X = \lbrace x_t, i=1 \dots n \rbrace$和$Y = \lbrace y_t, j=1 \dots m \rbrace$，则$X$和$Y$集合的相似性可以通过累计最小（最大）距离来度量，即：

\begin{equation} S(X, Y) = \sum_{i=1}^{i=n} \sum_{j=1}^{j=m} d_\min(x_i, y_j) \end{equation}

至于$d$选取何种距离，我们可以根据自己的应用场景来定夺，小白菜自己一般喜欢使用余弦相似度，因为该距离的计算最终可以转换成内积。累计最小（最大）距离应用的场景这里可以列举一二：

局部特征构成的两个集合，这里的局部特征不限于传统的局部特征，还可以是CNN构造的局部特征；
两个视频序列分别对视频帧提取全局特征，构成的两个视频帧特征集合，使用累计最小（最大）距离我们可以得到两个视频的相似性。

累计最小（最大）距离通常也是一种非对称性距离，在两个集合样本数量相差得比较大时，这种非对称性表现得非常明显。以上面所说的第二个例子为例，当两个视频由于某种不是很合理的取帧方式，导致两个视频取的帧数目相差比较大时，计算出的$S(X, Y)$和$S(Y, X)$会相差得很大，必然会导致其中的一个得到的相似度比较小。对于这种情形，在此相似性度量方式下，并没有特别好的办法来改善，所以在取帧的时候，尽量使两者的数目相当。

总体来说，累计最小（最大）距离对于度量两个集合的相似性是个不错的距离度量。下面讲讲对这个距离度量的计算速度优化问题。比如，我们要计算$X$和$Y$两个集合的相似性，并且每个集合有1000个元素，我们是要一个一个遍历计算找最小值然后相加吗？

显然这种计算方式太慢。前面提到过，在对$d$相似性度量的选取上，小白菜喜欢使用余弦相似性，矩阵乘法使得我们可以避免掉挨个遍历循环，通过矩阵相乘得到$X$和$Y$中各个样本与样本之间的相似性后，我们可以对相似性矩阵进行排序，然后求和相加即可得到$S(X, Y)$，即$X$和$Y$之间的相似性。

总结一下，在本篇博文中，分别从下面4个方面对计算机视觉中的非对称问题进行了探讨：