我想做又应该做的事,都会做到;我想做却不应做的事,都会戒掉。
Inner Product Layer
Inner Product Layer即全连接层,对于IP层的理解,可以简单的将其视为矩阵1*N和矩阵N*M相乘后得到1*M的维度向量。
举个简单的例子,比如输入全连接层的是一个3*56*56维度的数据,假设未知的权重维度为N*M,假设全连接层的输出为num_ouput = 4096,为了计算全连接层的输出,全连接层会将输入的数据3*56*56 reshape 成为1*N的形式,即1x(56x56x3) = 1x9408,所以:
N = 9408
M = num_ouput = 4096
由此,我们做了一个(1x9408)矩阵和(9408x4096)矩阵的乘法。如果num_output的值改变成为100,则做的是一个(1x9408)矩阵和(9408x100)矩阵的乘法。Inner Product layer(常被称为全连接层)将输入视为一个vector,输出也是一个vector(height和width被设为1)。下面是IP层的示意图
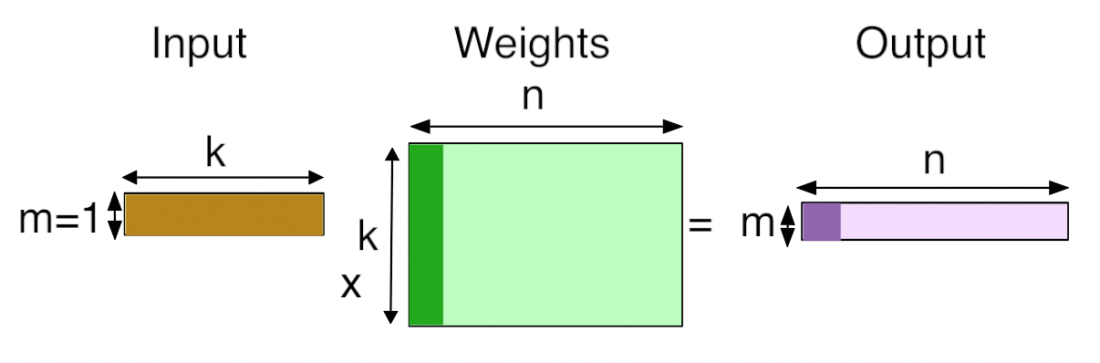
增大num_output会使得模型需要学习的权重参数增加。IP层一个典型的例子:
layer {
name: "ip1"
type: "InnerProduct"
bottom: "pool2"
top: "ip1"
# learning rate and decay multipliers for the weights
param {
lr_mult: 1
}
# learning rate and decay multipliers for the biases
param {
lr_mult: 2
}
inner_product_param {
num_output: 500
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
}
}
有了上面对IP层的理解,对caffe inner_product_layer.cpp中Forward的理解就比较自然了。下面是Caffe的IP层在CPU上的实现:
template <typename Dtype>
void InnerProductLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
const Dtype* weight = this->blobs_[0]->cpu_data();
caffe_cpu_gemm<Dtype>(CblasNoTrans, transpose_ ? CblasNoTrans : CblasTrans,
M_, N_, K_, (Dtype)1.,
bottom_data, weight, (Dtype)0., top_data);
if (bias_term_) {
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, N_, 1, (Dtype)1.,
bias_multiplier_.cpu_data(),
this->blobs_[1]->cpu_data(), (Dtype)1., top_data);
}
}
上面完成矩阵与矩阵相乘的函数是caffe_cpu_gemm<Dtype>(见math_functions.cpp),caffe_cpu_gemm函数矩阵相乘的具体数学表示形式为:
上式中TransX是对X做的一种矩阵变换,比如转置、共轭等,具体是cblas.h中定义的为枚举类型。在math_functions.cpp中,除了定义矩阵与矩阵相乘的caffe_cpu_gemm外,还定义了矩阵与向量的相乘,具体的函数为caffe_cpu_gemv,其数学表示形式为:
上面表达式中,y是向量,不是标量。
参考
- Why GEMM is at the heart of deep learning
- What is the output of fully connected layer in CNN?
- caffe_cpu_gemm函数
- Caffe学习:Layers
- Caffe Layers
GEMM
在上面的IP层中,我们已经涉及到了GEMM的知识,在这一小节里面,不妨对该知识点做一个延伸。
GEMM是BLAS (Basic Linear Algebra Subprograms)库的一部分,该库在1979年首次创建。为什么GEMM在深度学习中如此重要呢?我们可以先来看一个图:
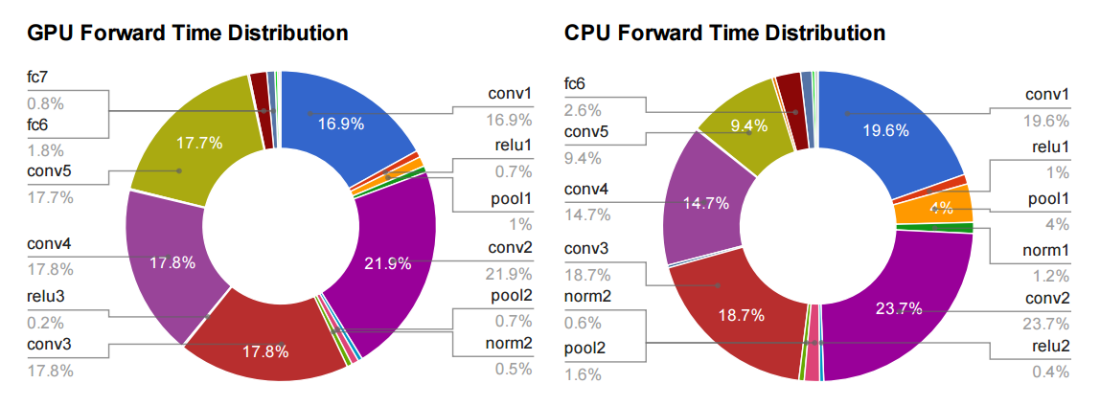
图片摘自Yangqing Jia的thesis
上图是采用AlexNet对CNN网络中不同layer GPU和CPU的时间消耗,从更底层的实现可以看到CNN网络的主要时间消耗用在了FC (for fully-connected)和Conv (for convolution),而FC和Conv在实现上都将其转为了矩阵相乘的形式。举个例子:
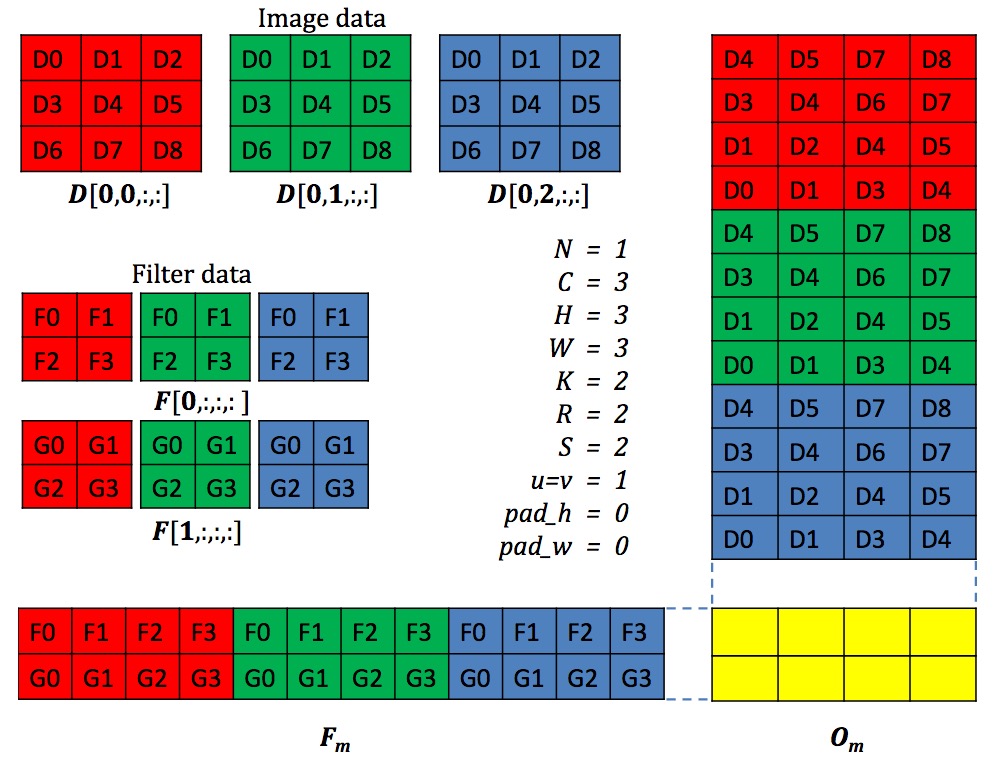
上面Conv在Caffe中具体实现的时候,会将每一个小的patch拉成一个向量,很多patch构成的向量会构成一个大的矩阵,同样的对于多个卷积核展成一个矩阵形式,从而将图像的卷积转成了矩阵与矩阵的相乘(更形象化的解释参阅在 Caffe 中如何计算卷积?)。上面可以看到在FC和Conv上消耗的时间GPU占95%,CPU上占89%。因而GEMM的实现高效与否对于整个网络的效率有很大的影响。
那么什么是GEMM呢?GEMM的全称是GEneral Matrix to Matrix Multiplication,正如其字面意思所表达的,GEMM即表示两个输入矩阵进行相乘,得到一个输出的矩阵。两个矩阵在进行相乘的时候,通常会进行百万次的浮点运算。对于一个典型网络中的某一层,比如一个256 row1152 column的矩阵和一个1152 row192 column的矩阵,二者相乘57 million (256 x 1152 x 192)的浮点运算。因而,通常我们看到的情形是,一个网络在处理一帧的时候,需要几十亿的FLOPs(Floating-point operations per second,每秒浮点计算)。
既然知道了GEMM是限制整个网络时间消耗的主要部分,那么我们是不是可以对GEMM做优化调整呢?答案是否定的,GEMM采用Fortran编程语言实现,经过了科学计算编程人员几十年的优化,性能已经极致,所以很难再去进一步的优化,在Nvidia的论文cuDNN: Efficient Primitives for Deep Learning中指出了还存在着其他的一些方法,但是他们最后采用的还是改进的GEMM版本实现。GEMM可匹敌的对手是傅里叶变换,将卷积转为频域的相乘,但是由于在图像的卷积中存在strides,使得傅里叶变换方式很难保持高效。





